Problems

HRW 21-13

In this problem we are given two charges ($q_1$, $q_2$) placed on the $x$-axis and are asked to place a third charge, $q_3$ in a place where it will experience no force. If $q_3$ is placed anywhere off the $x$-axis the two forces on it due to the other charges will be in different directions and therefore have no hope of canceling (See Fig. 1). Thus, $q_3$ must be placed on the axis.

Figure 1: Forces on $q_3$ are not collinear when off axis.

Now, $q_3$ must be placed on the axis, but there are now 3 possible regions to consider. These regions (I, II, and III) are separated by $q_1$ and $q_2$. Assume that $q_3$ is positively charged. If it is placed in region II, then both forces on it would be to the right. Thus, they can never cancel in this region.

This leaves I and II. Now, in both regions, the forces will be in different directions, so we have the possibility of cancellation. Now, if were' in III, we're always closer to $q_2$, which is the larger charge. Since the electric force is proportional to charge and inversely proportional to separation squared (see the equation above), the force due to $q_2$ will always dominate in III, so there will be no place where the net force goes to zero.

This leaves only region I. In this region we're always closest to $q_1$, which is the weaker of the two charges. Thus we may expect a cancellation in this region. If we place the third charge a distance $x$ from the axis, then the total force on it from the two charges will be

$$\begin{eqnarray*} F &=& F_{31}+F_{32} \\ &=& k\frac{q_1q_2}{x^2}+ k\frac{q_2q_3}{(x+L)^2}=0. \end{eqnarray*}$$

Thus we can cancel $k$ and $q_2$ to get

$$\frac{q_1}{x^2}+ \frac{q_3}{(x+L)^2}=0.$$

Cross-multiplying and collecting terms in $x$ gives the quadratic equation

$$x^2(q_1+q_3)+x(2Lq_1)+q_1L^2=0$$

and the (complicated looking) solutions are

$$x=L\left( \frac{-q_1\pm\sqrt{q_1^2-q_1(q_1+q_2)}}{q_1+q_2} \right).$$

What is interesting about this solution is that it depends linearly on $L$. This means that as long as $\vert q_2\vert>\vert q_1\vert$ we will have a solution somewhere in region I for any given value of $L$. This was not obvious from the setup of the problem, but is nevertheless true. It can also be seen from the following graph of the magnitudes of the forces from charges 1 and 2 (Fig. 2). In region I the two curves intersect, and this point is where the net force goes to zero. Convince yourself that by sliding $q_2$ around, as long as it stays to the left of $q_1$, the two graphs will always intersect somewhere in I. (How does this solution depend on $q_1$? On $q_3$?)

Figure 2: Force magnitudes due to $q_1$ and $q_2$ and their cancellation in I.

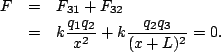
Now that you've seen this solution in detail, you should be able to check what happens in the following cases:

1. $\vert q_1\vert=\vert q_2\vert$.
2. $q_1$ negative and $q_2$ positive.
3. $q_1$ and $q_2$ with the same sign.

Finally, here is a graph of the net force in each region along the $x$-axis (Fig. 3). If the force is positive then it is toward the right, and if it is negative it is to the left (indicated by the arrows). The forces does cross the axis at $x=.137$, but it's invisible because of the scale of the plot.

Figure 3: Net force on $q_3$ as a function of $x$.