Moments

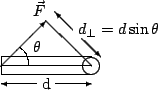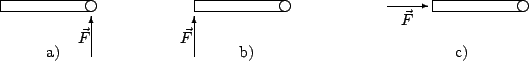
By now we're very familiar with Forces. A Force is something that causes an object move. More specifically if I apply a force in a certain direction it will cause the object to move (accelerate) in that direction. But objects can do more than just move in a certain direction, they can rotate as well. Just as the cause of linear motion is a force, the cause of a rotation is called a moment (or torque).

A moment is caused by a force, but it is more than a force. It depends on where and in what direction a force is applied. For example, you know that you will never open a door by pushing at the hinge (Fig. 1a), and the farther away from the hinge you push the easier it is to open (Fig. 1b). Moreover, if you push far away from the hinge, but push straight toward the hinge, the door isn't going to open either (Fig. 1c).

$$\begin{array}{c@{\hspace{.5in}}c@{\hspace{.5in}}c} \begin{pi... ...ut(8,7){$\vec{F}$} \put(20,0){c)} \end{picture} \\ \end{array}$$

Figure 1. Forces applied in different places on a door. The hinge is on the right.

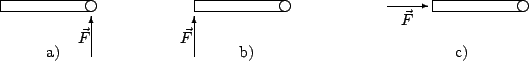
As cases b and c above illustrate, the moment applied by a force depends on the angle the force makes with the hinge. In fact, we can easily write down precisely what this dependence is by taking our force and writing it into components - one perpendicular to the door and one parallel to it. Then we have exactly are two cases above - one force that has maximal moment and another which has zero. If the force makes angle $\theta$ with the axis of the door, then the perpendicular component is

$$F_{\perp}=F\sin\theta$$

And finally, since the moment is greater the further away we push from the hinge, we have for the moment

$$m=F_{\perp}\times d = Fd\sin\theta$$

where $d$ is the distance from where the force is applied and the hinge (See Fig. 2).

$$\begin{picture}(50,30) \put(10,10){\line(1,0){20}} \put(10,1... ...,0){8}} \put(22,8){\vector(1,0){8}} \put(19,7){d} \end{picture}$$

Figure 2. Perpendicular and Parallel components of a force.

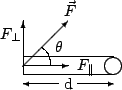
Note that that we can regroup the above expression in a different way:

$$m=F(d\sin\theta)=F\times d_{\perp}$$

where $d_{\perp}$ is called the moment arm. It is the perpendicular (shortest) distance between the force vector and the hinge.

$$\begin{picture}(50,30) \put(10,10){\line(1,0){20}} \put(10,1... ...or(1,-1){4}} \put(27,19){$d_{\perp}=d\sin\theta$} \end{picture}$$

Figure 3. Moment arm demonstrated.

This means that the force has an ''effective`` distance $d_{\perp}$ for the exertion of the moment. It is as if the force was applied at a distance of $d_{\perp}$ away from the hinge and at a right angle.