
|
Now, what we need to calculate is the time coordinate in all three
reference systems of when the messenger reaches the front of the
armada. Since this is an event in space-time, all we need to do is
calculate the time in one coordinate system and then convert it to the
others using Lorentz transformations. I will do the calculations in
the stationary ![]() frame an then transform to the others.
frame an then transform to the others.
As seen by ![]() , the messenger starts at the origin and then moves with
, the messenger starts at the origin and then moves with
![]() until it reaches the front of the armada. But the armada is
also seen to be moving with speed
until it reaches the front of the armada. But the armada is
also seen to be moving with speed ![]() . So the ship has to
move the length of the armada and move an extra distance since the
armada is moving.
. So the ship has to
move the length of the armada and move an extra distance since the
armada is moving. ![]() will judge this to take a time
will judge this to take a time ![]() . Let us
denote the total distance moved as
. Let us
denote the total distance moved as ![]() (as judged by
(as judged by ![]() ). Then we have
). Then we have
Now that we've established that relationship we can solve for ![]() once
we know the length
once
we know the length ![]() of the armada as measured by
of the armada as measured by ![]() . The armada
will be length contracted (it is moving as seen by
. The armada
will be length contracted (it is moving as seen by ![]() ), so we have
), so we have
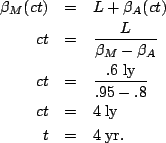
Now we need to know the ![]() coordinate of this event before we can
transform it to the other systems. We have (substituting), that
coordinate of this event before we can
transform it to the other systems. We have (substituting), that
So the hard work is done. Now we use the Lorentz transformations
(again, being careful to use the right ![]() 's)
's)


As an exercise to the reader, find ![]() and
and ![]() . What do these mean?
. What do these mean?