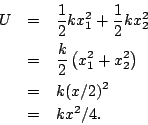

Next: 15-28.
Up: Energy I: Week 1
Previous: 15-8.
This one is a bit tricky since it's not obvious how to
apply the results we have for spring systems to this case. There are
a few different ways to look at this, but consider the following.
Both springs have the same spring constant, 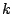 . If we move the mass
to the left, symmetry demand than both springs stretch by an equal
amount. So if the distance of the mass from equilibrium is
. If we move the mass
to the left, symmetry demand than both springs stretch by an equal
amount. So if the distance of the mass from equilibrium is 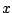 , and
of the two springs
, and
of the two springs 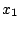 and
and 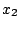 , then
, then 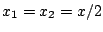 . Now, the
potential energy of the two spring system is given by:
. Now, the
potential energy of the two spring system is given by:
Thus the force is
So that the effective spring constant is cut in half. Thus the new
frequency of oscillations will be given by
where 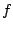 would be the frequency if only one spring were present.
would be the frequency if only one spring were present.
This result should make sense: if a spring is made longer, then a
given stretch of that spring is spead out over the the spring more.
Thus there is less stress on each part of the spring and less force.
Thus the overall spring constant is decreased. From the above formula
we see that this descrease is linear, that is
for a given material composition, where 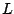 is the spring length.
is the spring length.


Next: 15-28.
Up: Energy I: Week 1
Previous: 15-8.
Dan Cross
2006-10-18