

|
| Research |
Publications
|
|
Luis Cruz Cruz: Current Research
|
|
Neurons function and communicate using vast networks of connections that exist within the three dimensional arrangement of the brain. We strive to understand how the topology of the physical arrangement of neurons modulates the firing dynamics of neurons. This topology goes beyond random placements of neurons since there exist organized structures and correlations in the connectivity. We use computational methods to model and understand the role of number and strength of neuronal connections, cluster connectivity, distances, and topology on the dynamics of the network. We also study the effect of damaging the network with the purpose of understanding the nature of normal aging and neurological conditions such as Alzheimer's disease and traumatic brain injury. |
| Traveling waves in 1D | |
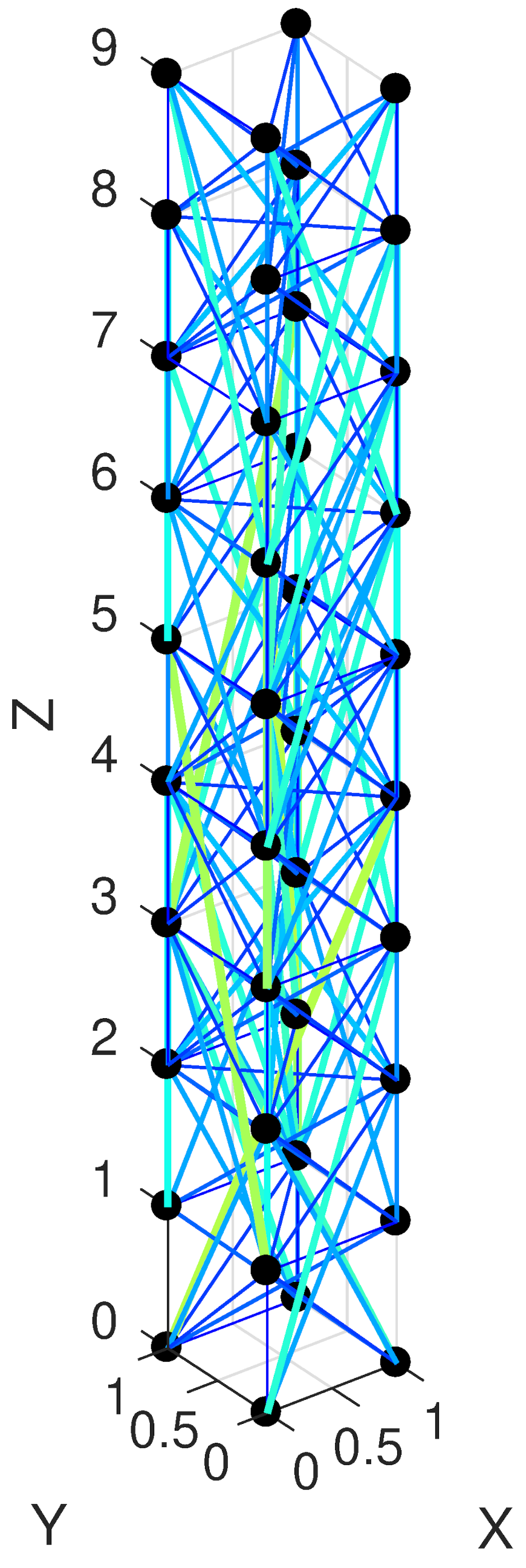
When groups of connected neurons fire together, they can evoke excitations in their neighbors that in turn can evoke further excitations to farther neighbors. This cascade of excitations can create a traveling wave of neuronal spikes. Traveling waves have been observed in the cortex of mammalian brains and in vitro. Their specific function, however, remains unknown. Although typically these traveling waves are observed on the surface of the brain as two dimensional waves, there is no a priori reason that prevents their observation in other dimensions. Mini or microcolumns are cellular structures in the frontal cortex perpendicular to the pial surface that span the width of the cortex. These one dimensional structures are hundreds of micrometers long with connected neurons that we hypothesize can support traveling waves. In a computational study of locally connected neurons using the Izhikevich neuronal model we study the properties of these propagating spikes in one dimension. We show that these waves can be spontaneously created from random small background stimulus and when two such waves traveling in opposite directions meet each other they annihilate. Their wave velocity is determined by both the propagation speed of the action potential and the neuron dynamics. We also found that inhibitory neurons in the microcolumn can nonintuitively serve to both give rise to traveling waves and to inhibit neuronal activity of already formed waves that travel over these inhibitory neurons. 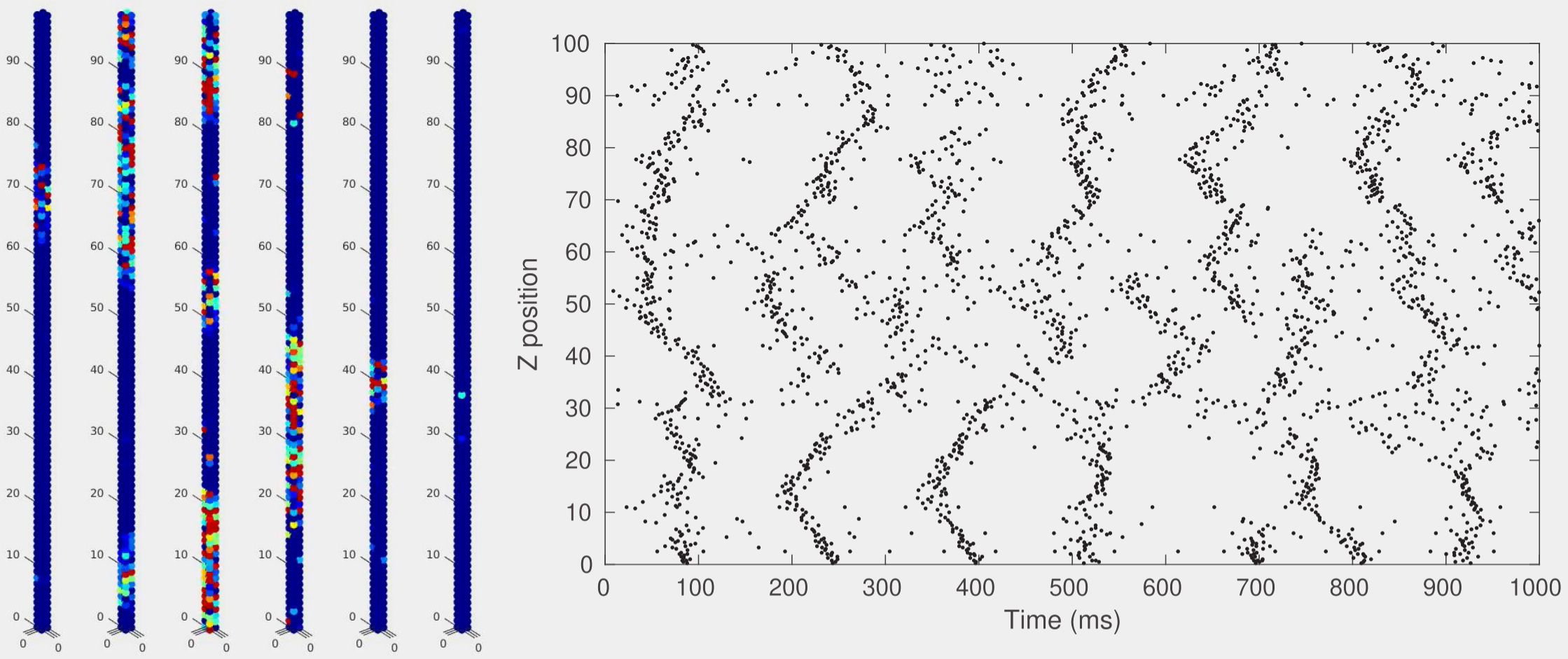
|
|
| See here for more details. | |
|
Synchronization in networks of clustered neurons |
|
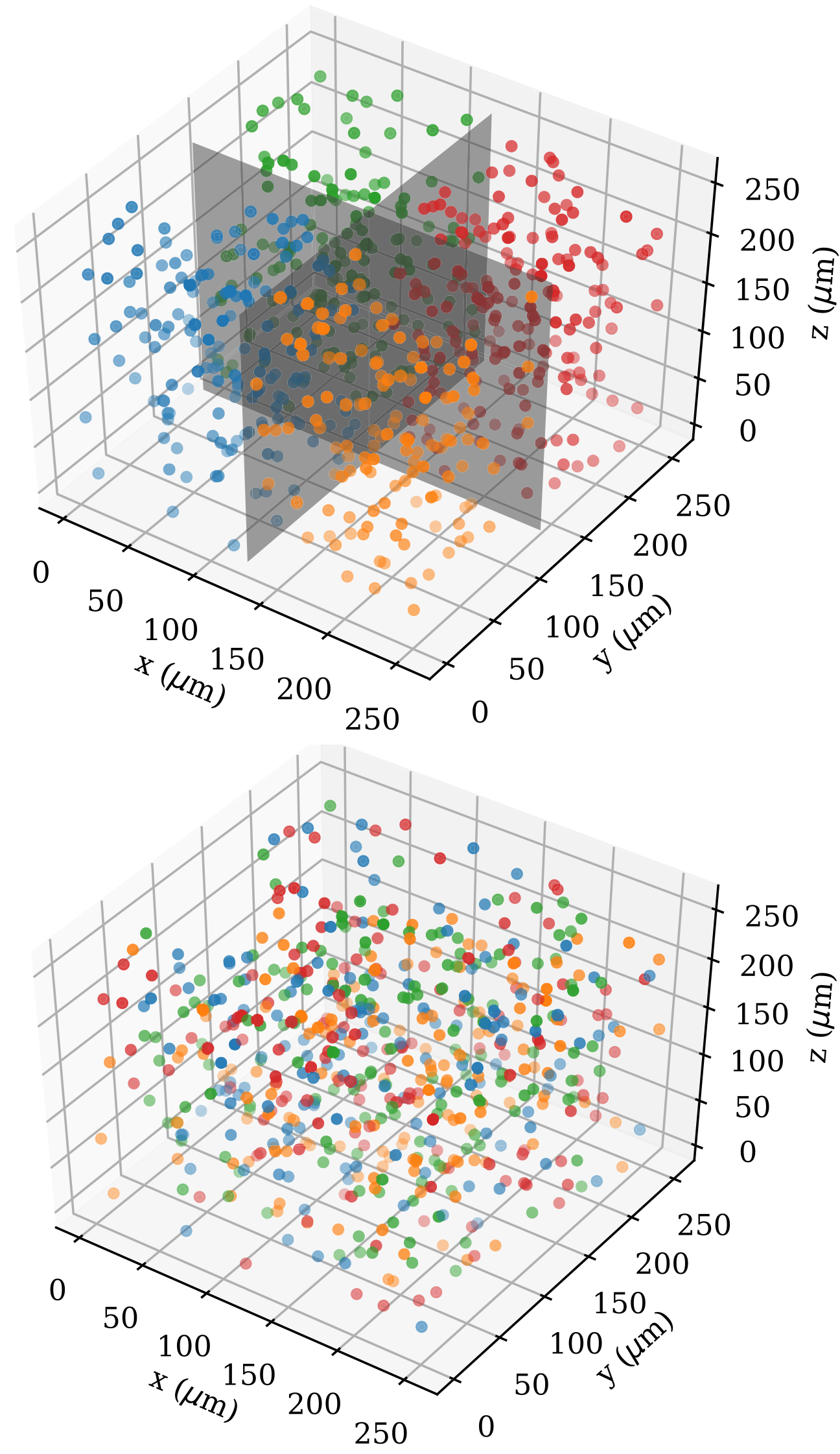
Connectivity between neurons in the brain is nonrandom. Function of neuronal networks in many cases can be correlated to the structure of networks. Clustered neurons have been shown to not only exist in the brain, but also to be synaptically connected possibly engaging in basic computational function. Because signals between neurons, or spikes, take time to travel from one neuron to another, the physical structure of networks is important as it is this topology that dictates the time delays of the whole network. Because synchronized firing of neurons depends on the arrival time of signals, the topology of networks can modulate synchronicity. By utilizing computational models of neuronal networks, we study the effect of topology on the synchronized firing of neurons modeled by the Hodgkin-Huxley model and connected using a stochastic block model with clusters of tunable neuronal connectivity and distance-dependent signal delay times. Our results suggest that networks with neurons connected in a grid have a higher degree of synchrony than a randomly connected network. 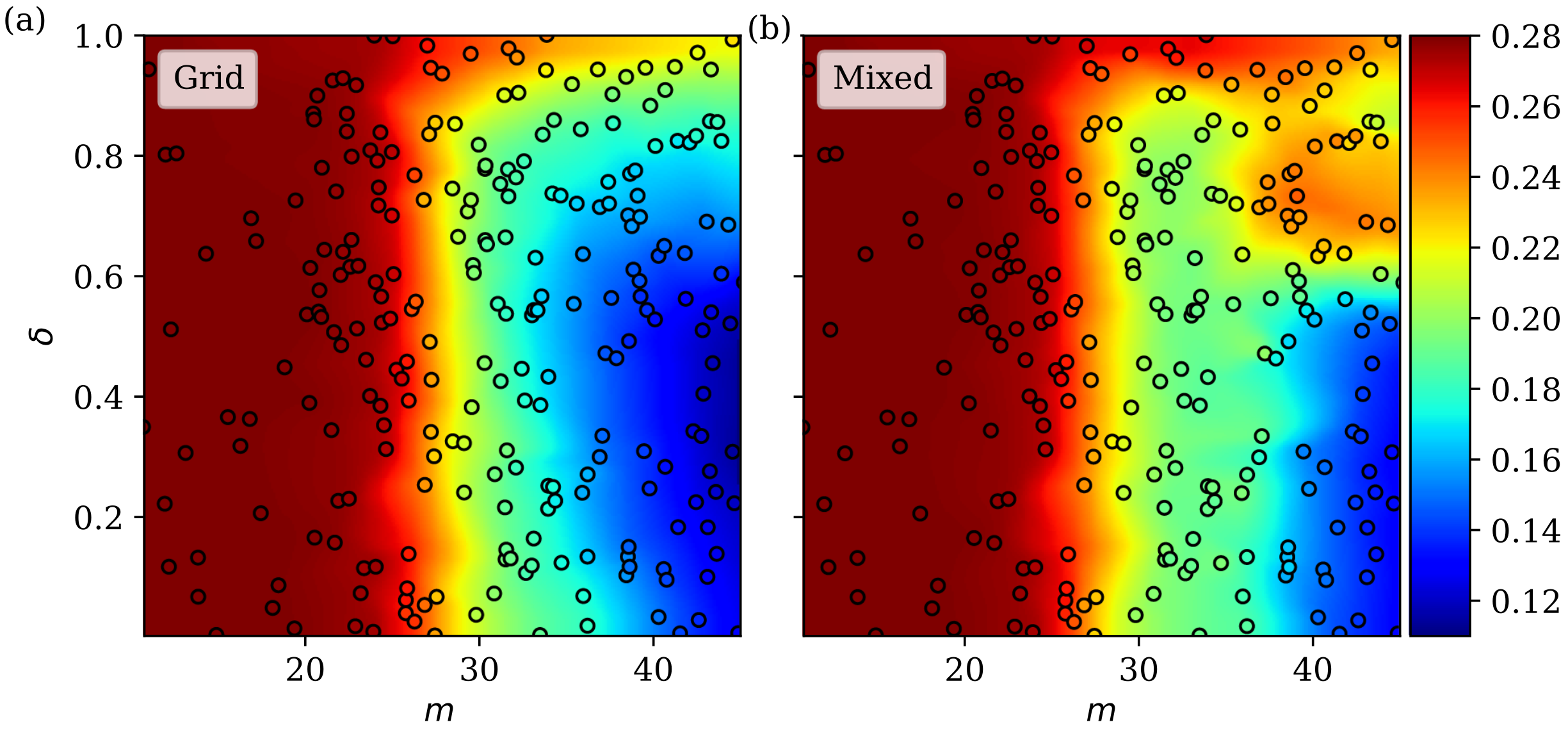
|
|
| See here for more details. |
|
|